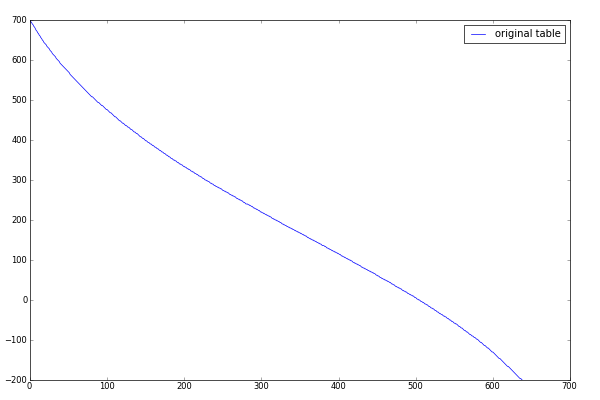
The firmware contains a big table (824 numbers, 1648 byte), used to convert RCX temperature sensor input to degree. John Hansen notices that the whole table is not even used because input value is clipped to usable interval. Here is the original code:

if (InputVal < 290)
  InputVal = 290;
else if (InputVal > 928)
  InputVal = 928;
InputVal = TempConvTable[(InputVal) - 197];

As you can see, the index can not be lower than 93, and higher than 731. John Hansen made a change to get rid of unused values.

But this table could be removed completely! By looking at the table values, it looks like it can be approximated by a polynomial. Here is a graph of table values:

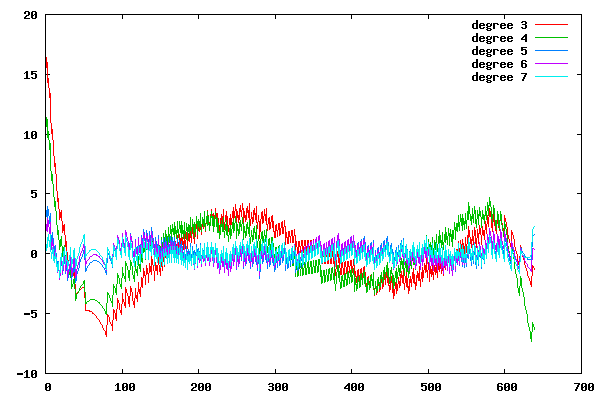
I used Gnuplot to find the polynomial. I tried with several polynomial degrees to find which will be precise enough. Here is the gnuplot script, the "num" file contains the table values:

set style data line
f3(x) = k33 * x**3 + k32 * x**2 + k31 * x + k30
fit f3(x) 'num' via k33, k32, k31, k30
f4(x) = k44 * x**4 + k43 * x**3 + k42 * x**2 + k41 * x + k40
fit f4(x) 'num' via k44, k43, k42, k41, k40
f5(x) = k55 * x**5 + k54 * x**4 + k53 * x**3 + k52 * x**2 + k51 * x + k50
fit f5(x) 'num' via k55, k54, k53, k52, k51, k50
f6(x) = k66 * x**6 + k65 * x**5 + k64 * x**4 + k63 * x**3 + k62 * x**2 + k61 * x + k60
fit f6(x) 'num' via k66, k65, k64, k63, k62, k61, k60
f7(x) = k77 * x**7 + k76 * x**6 + k75 * x**5 + k74 * x**4 + k73 * x**3 + k72 * x**2 + k71 * x + k70
fit f7(x) 'num' via k77, k76, k75, k74, k73, k72, k71, k70
#plot 'num', f3(x), f4(x), f5(x), f6(x), f7(x)
plot 'num' using ($1-f3($0)) title "degree 3", \
    'num' using ($1-f4($0)) title "degree 4", \
    'num' using ($1-f5($0)) title "degree 5", \
    'num' using ($1-f6($0)) title "degree 6", \
    'num' using ($1-f7($0)) title "degree 7"

And the resulting graph:

The fifth degree seems to be good enough (maximum of 0.4 degree error compared to original value). Actually, I do not think that the sensor is that precise.

Here are the coefficients that Gnuplot found:

rms of residuals      (FIT_STDFIT) = sqrt(WSSR/ndf)    : 0.908094
variance of residuals (reduced chisquare) = WSSR/ndf   : 0.824636

Final set of parameters            Asymptotic Standard Error
=======================            ==========================

k55             = -1.92723e-11     +/- 2.818e-13    (1.462%)
k54             = 3.29031e-08      +/- 4.518e-10    (1.373%)
k53             = -2.37558e-05     +/- 2.614e-07    (1.1%)
k52             = 0.00914337       +/- 6.572e-05    (0.7187%)
k51             = -2.92203         +/- 0.006753     (0.2311%)
k50             = 695.823          +/- 0.2126       (0.03056%)

Now the table can be replaced by a function which calculate the table value using this polynomial. Every coefficient is multiplied by 2⁴⁸, to keep integer math.

SWORD cInputTempConv(UWORD InputVal)
{
  static const long long TempCoeff[] = { -5425ll, 9261399ll, -6686663252ll,
    2573629857807ll, -822478326197838ll, 195856762719738784ll };
  const unsigned int TempCoeffShift = 48;
  /* Replace the original table with polynomial. */
  int i;
  long long Input = InputVal;
  long long Output = TempCoeff[0];
  for (i = 1; i < sizeof TempCoeff / sizeof TempCoeff[0]; i++)
    Output = Output * Input + TempCoeff[i];
  /* Round. */
  return Output + (1ll << TempCoeffShift - 1) >> TempCoeffShift;
}

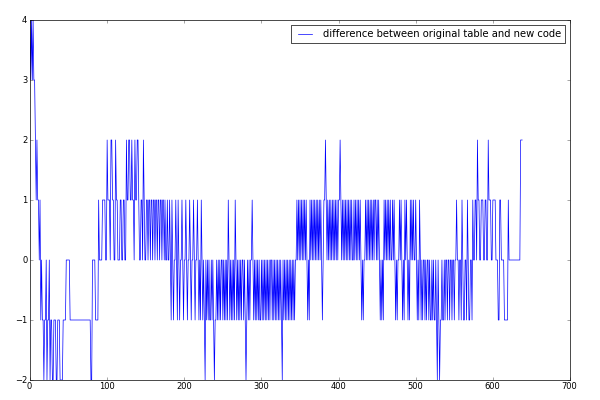
Here is the difference between this code and the original table:

The change is made in 8aa1d4b3.